Now You’re Cooking with DAGs!

Vaibhav Sagar

@vbhvsgr

Drawing a Git repository

All Git commit graphs are DAGs

Here’s a DAG

Here’s a not-DAG

What I need

Determinining DAGness

Highlighting not-DAG bits

Processing vertices in some order

How???

StackOverflow search

Source: https://stackoverflow.com/questions/583876/how-do-i-check-if-a-directed-graph-is-acyclic

Topological sort

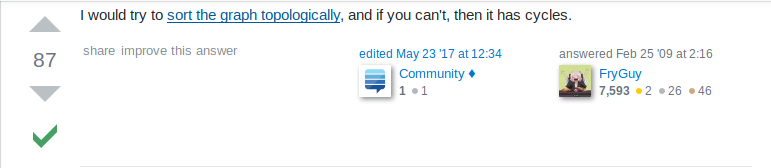
Source: https://stackoverflow.com/questions/583876/how-do-i-check-if-a-directed-graph-is-acyclic

Topological sort

Source: https://upload.wikimedia.org/wikipedia/commons/c/c6/Topological_Ordering.svg

SCCs

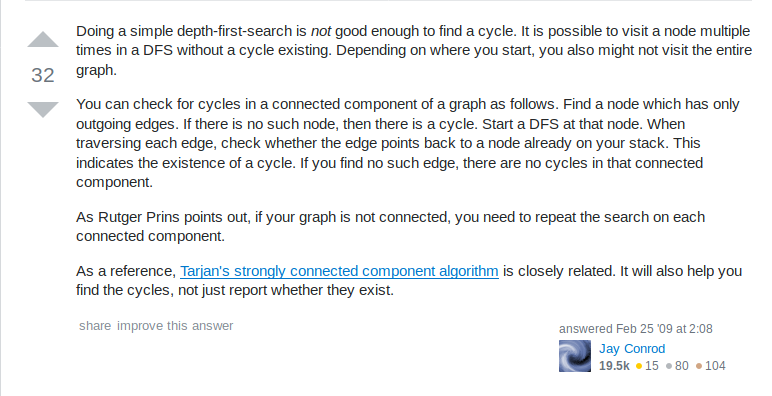
Source: https://stackoverflow.com/questions/583876/how-do-i-check-if-a-directed-graph-is-acyclic

SCCs

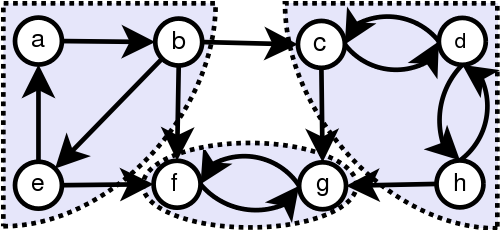
Source: https://upload.wikimedia.org/wikipedia/commons/5/5c/Scc.png

Tarjan’s Algorithm

 algorithm tarjan is
  input: graph G = (V, E)
  output: set of strongly connected components (sets of vertices)

  index := 0
  S := empty array
  for each v in V do
    if (v.index is undefined) then
      strongconnect(v)
    end if
  end for

  function strongconnect(v)
    // Set the depth index for v to the smallest unused index
    v.index := index
    v.lowlink := index
    index := index + 1
    S.push(v)
    v.onStack := true

    // Consider successors of v
    for each (v, w) in E do
      if (w.index is undefined) then
        // Successor w has not yet been visited; recurse on it
        strongconnect(w)
        v.lowlink  := min(v.lowlink, w.lowlink)
      else if (w.onStack) then
        // Successor w is in stack S and hence in the current SCC
        // If w is not on stack, then (v, w) is a cross-edge in the DFS tree and must be ignored
        // Note: The next line may look odd - but is correct.
        // It says w.index not w.lowlink; that is deliberate and from the original paper
        v.lowlink  := min(v.lowlink, w.index)
      end if
    end for

    // If v is a root node, pop the stack and generate an SCC
    if (v.lowlink = v.index) then
      start a new strongly connected component
      repeat
        w := S.pop()
        w.onStack := false
        add w to current strongly connected component
      while (w != v)
      output the current strongly connected component
    end if
  end function