A pointer to n possible locations needs log₂n bits

Data structures with n items need O(nlog₂n) space for pointers!

The rent is too damn high!

Unlabeled binary trees only need 2n + o(n) bits

One approach: balanced parentheses?

Better space usage, but inefficient to use

How do we get efficient space usage and efficient operations?

Metrics for space and time

• Space: measured in bits
• Time: measured in bit-accesses

Rank

rank_e(S, i): The number of es at or before index i

Select

select_e(S, i): The index of the ith e

Time complexity

• O(log₂n) at the time of writing, O(1) now!

More resources

• Succinct indexable dictionaries with applications to encoding k-ary trees and multisets
• Fast, Small, Simple Rank/Select on Bitmaps
• Space-Efficient, High-Performance Rank & Select Structures on Uncompressed Bit Sequences

Rank/Select beyond bitmaps

• Wavelet Trees for All

Implicit bitmap

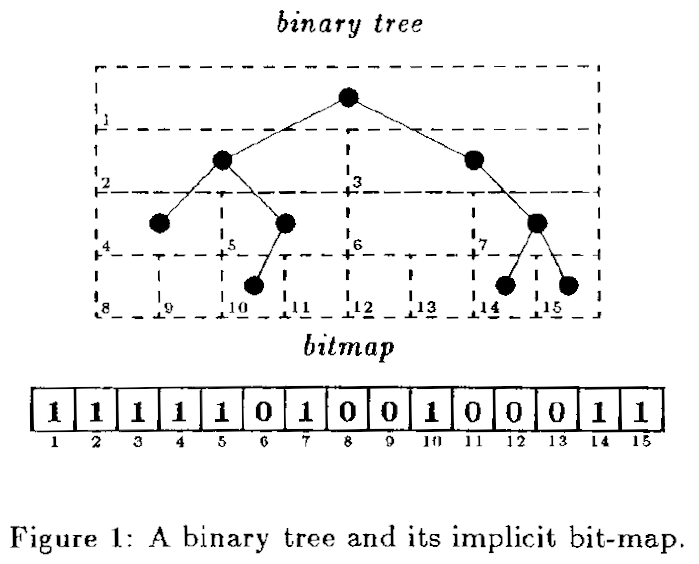
Level-order binary marked

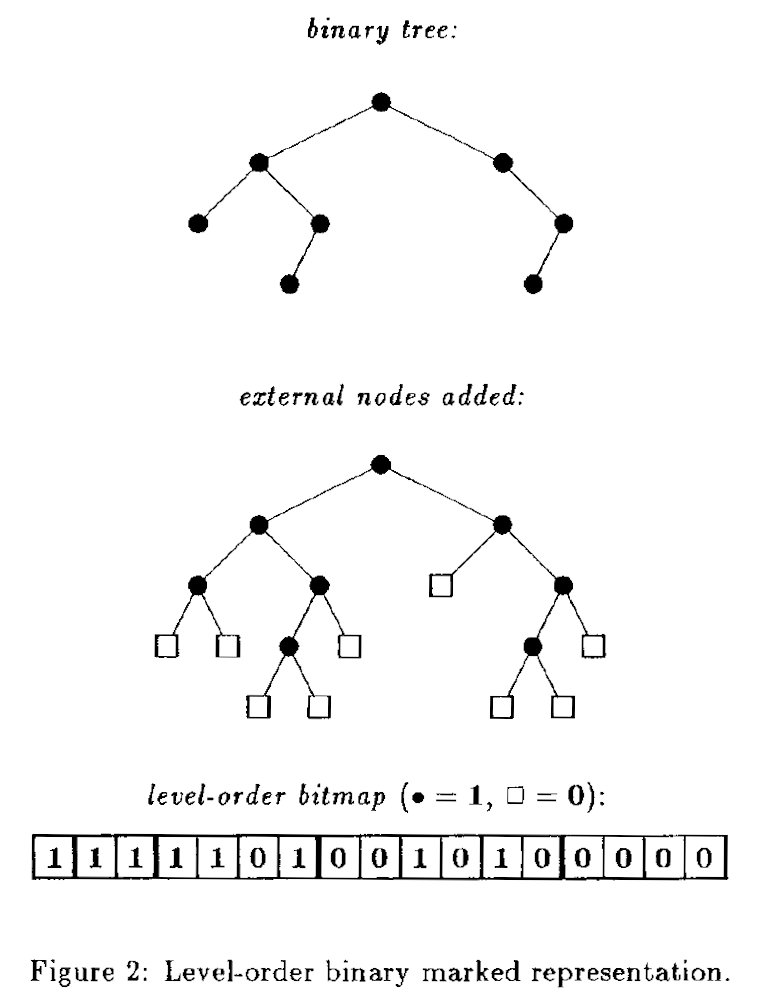
Level-order binary marked

• left-child(m) = 2 ⋅ rank(m)
• right-child(m) = 2 ⋅ rank(m) + 1
• parent(m) = select(⌊m/2⌋)

Level-order unary degree sequence

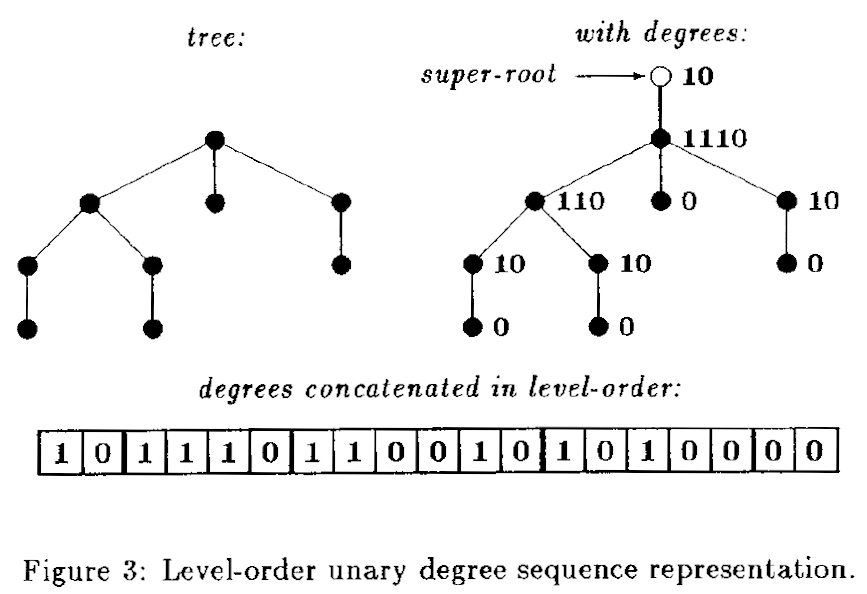
Level-order unary degree sequence

• first-child = select₀(rank(m)) + 1
• next-sibling = m + 1
• parent(m) = select(rank₀(m))

Parentheses balancing

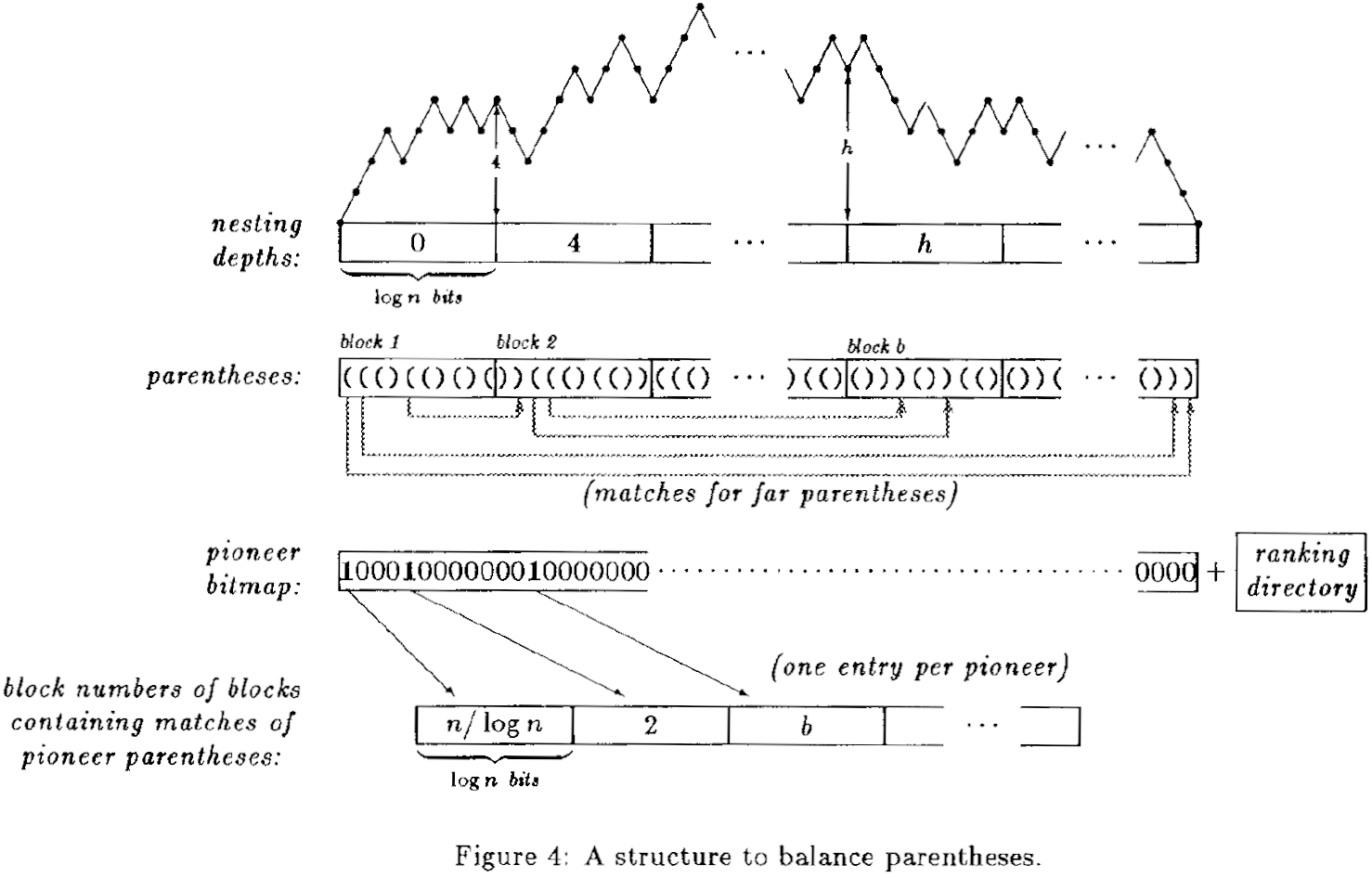
Bounded pagenumber graphs

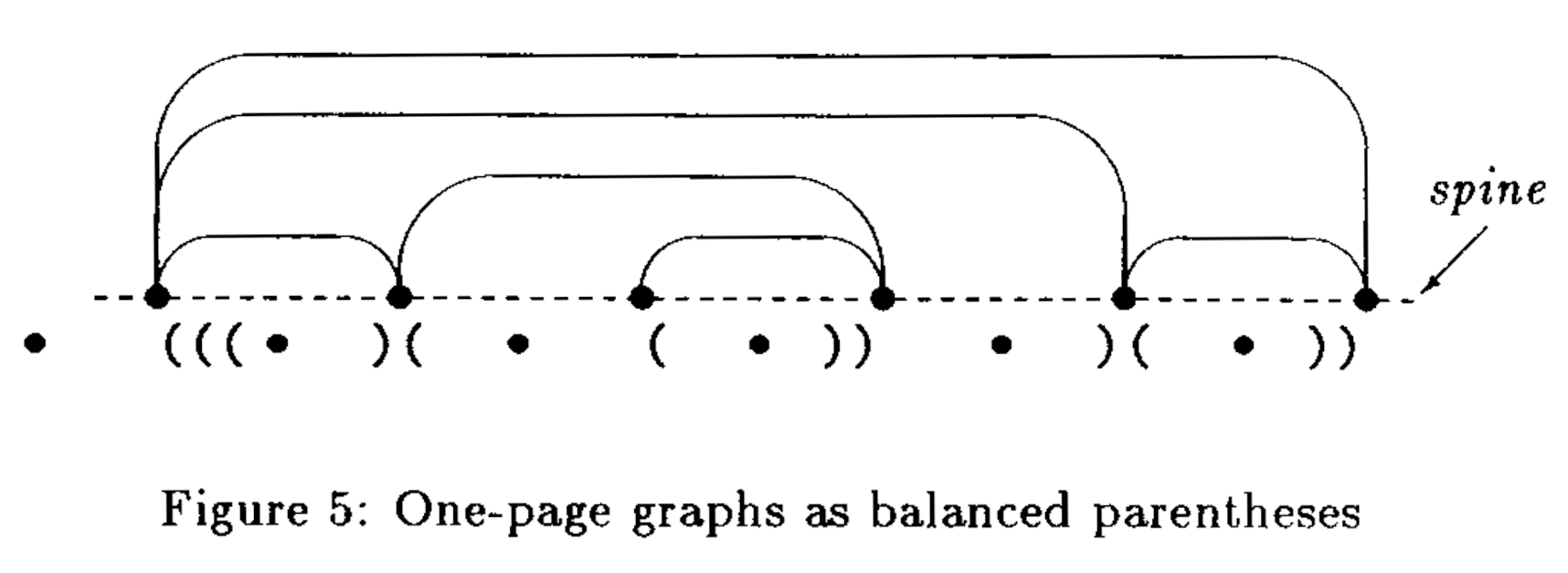
Bounded pagenumber graphs

• node-to-edge(m) = rank₀(select(m) + 1)
• edge-to-node(e) = rank(select₀(e))

Semi-indexing

Compact Data Structures

This presentation

These slides are at https://vaibhavsagar.com/presentations/space-efficient-static-trees-graphs